索引:基础篇
索引概述

索引的主要内容主要涉及四个问题:
索引相关的面试内容基本离不开这四个问题,也就是说这四个问题基本涵盖了索引的所有核心内容;在实际工作的时候就需要利用这些基本知识来对索引出现的问题进行排查,这部分内容可以选择性学习,我会详细讲述几个常见的索引问题,剩下的可以去看《MySQL 实战 45 讲中的内容》
注:其实其他所有知识也都是可以按照这个思路去学习的,这样会非常方便你去理清知识的脉络,从而形成完整的知识体系
初识索引
索引本质就是采用数据结构实现的用于加快查询速度的类似于目录的结构
注:这个索引的定义是我根据自己的理解总结的,如果存在问题也请指出
直接给出索引的定义可能并不是特别好理解,那么我用字典这个例子来解释可能就比较好理解索引究竟是什么了:
我们在使用字典查询汉字的时候肯定不会每页挨着挨着去翻这个汉字在哪里,而是通过目录查询到这个汉字所在的页号后再翻到对应的页号从而找到这个汉字;数据库的使用和字典的使用过程基本相似,每次查询行记录的时候都会先通过索引(目录)找到这个行数据所在的数据页,然后在数据页中开始遍历从而找到符合要求的行记录
字典目录查询汉字的时候通常会有声母查询、偏旁查询、笔画查询这三种方式;数据库中的索引类型也可以和字典的目录使用方式相类比:声母查询几乎是最容易使用的查询方式,也是查询精度最高的方式,可以和数据库中的聚簇索引进行类比;偏旁查询和笔画查询通常需要联合使用,因为它们没有办法独立定位到唯一的汉字,可以和数据库中的非聚簇索引进行类比
注:字典这个例子本质上应该是哈希索引,大多数数据库的存储引擎都是采用 B+ 树索引,这两者的区别之后会提到
在索引的定义中已经提到其本质就是用于加速查询过程的:如果数据量比较小,那么无论是否使用索引,查询效率可能都不会有太大的变化;但是如果数据量非常大,那么在没有索引加速查询的情况下,每次查询数据都需要全表扫描,这就会造成系统的响应时间特别慢,对于用户来说是不可以接受的
索引实现
在开始了解实现索引的数据结构之前,先要了解两个基本的概念:
- 等值查询:查询得到的结果是唯一的
- 范围查询:查询得到的结果是集合
不同的数据结构对于这两种查询方式的支持程度不同,有些数据结构仅支持等值查询,而有些数据结构则是两种查询方式都支持
-- 前者显然是等值查询, 后者显然是范围查询 |
索引这种数据结构不是直接按照行记录进行组织的,而是按照数据页进行组织,在每个数据页中包含复数条行记录;不过,不知道这个概念其实并不是很影响之后的理解,并且为了方便起见之后还是认为是直接按照行记录进行组织的
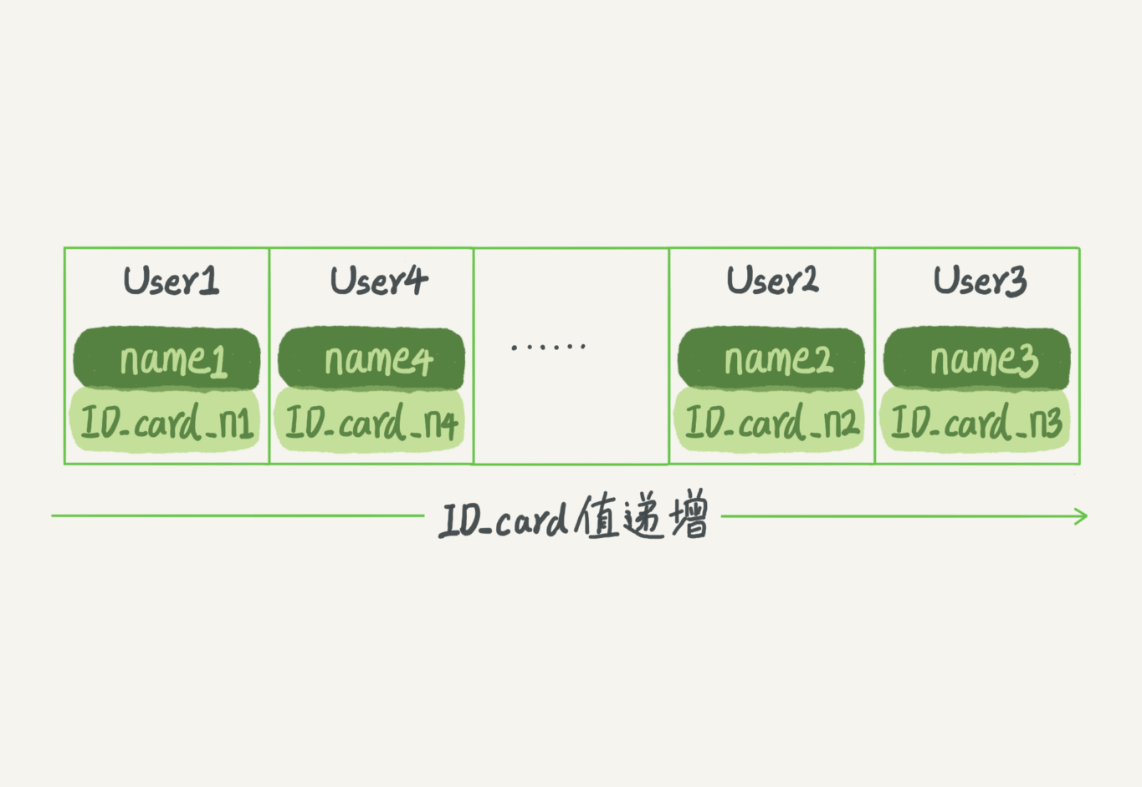
有序数组
将所有数据都按照递增或者递减的顺序进行排列,然后就可以采用二分查找来进行查询
在有序数组中使用二分查找,时间复杂度可以达到 O(logn) 级别,可以说是查询速度最快的数据结构,并且支持范围查询
但是每次插入或者删除数据的时候也就意味着有序数组中的记录也需要变化,数据中元素的删除效率显然是很低的
注:通常静态存储引擎,也就是数据库或者表中的数据几乎不怎么变的时候才会采用这种数据结构实现索引
哈希表
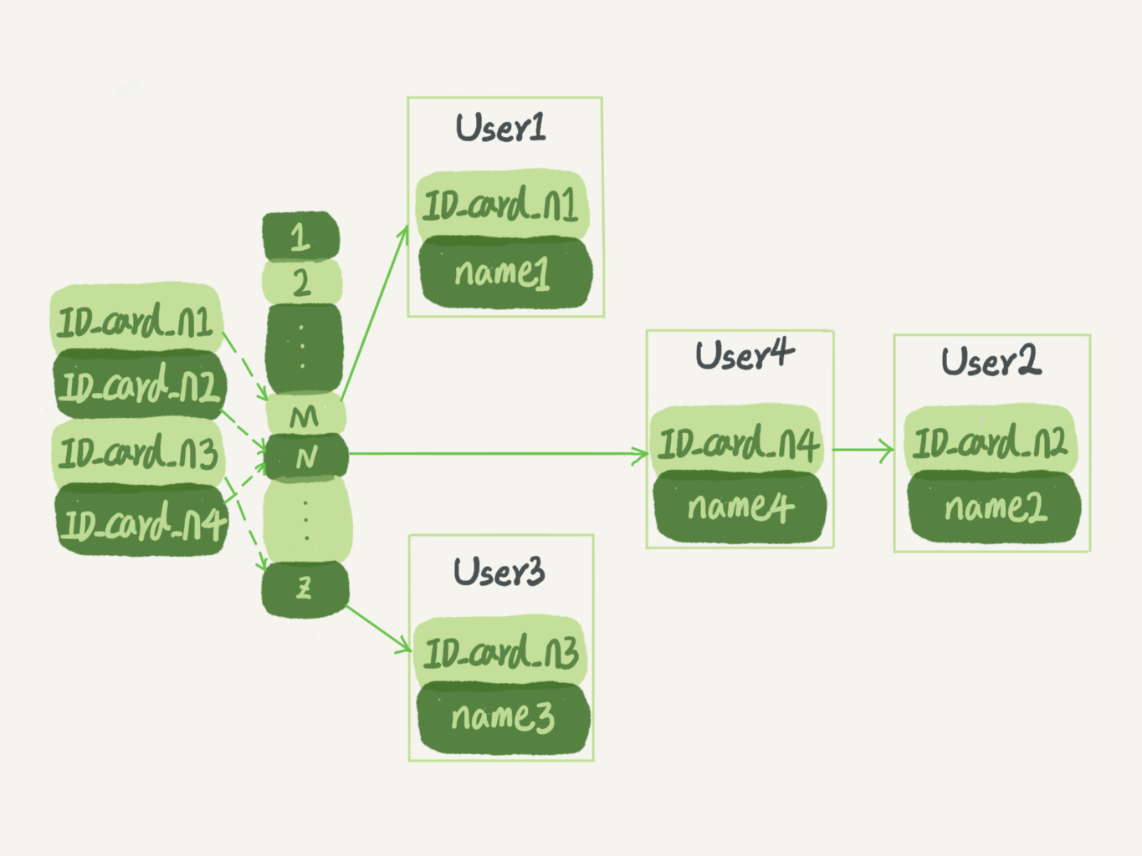
每次添加数据的时候就采用哈希函数计算出 key 的哈希值,然后将哈希值转换为索引从而将 key-value 放在对应的桶中(链表)
每次查询的时候也会计算出 key 对应的哈希值,然后找到对应的桶之后开始遍历从而找到符合条件的
- 如果是等值查询,那么找到符合条件的数据之后就结束查询
- 如果是范围查询,那么就重复这个查询过程,直到找到所有满足条件的数据
注:这部分建议直接去看哈希表相关的内容,这里只会简单进行解释
哈希表的查询速度理论上可以达到常数级,但是由于哈希冲突的存在,这个常数会相对比较大
但是常规实现的哈希表中所有元素都是无序的,那么就意味着在执行范围查询的时候,对于查询范围中的每个元素都需要单独重新去查询哈希表,相当于不支持范围查询
注:这里可能不太好理解为什么哈希表不支持范围查询,这里简单举个例子来解释下:select * from t where id between 2 and 5
- 因为所有数据都是通过哈希函数映射到桶中(链表),而在桶中的数据并不会都会满足查询条件
- 所以在查询到第一条符合要求的数据后没有办法继续向后遍历得到剩下符合要求的数据
- 也就是说,在查询到 id = 2 的数据之后只能够重新进行查询流程而无法向后遍历找到 id = 3、4、5 的数据
- 这也是为什么说哈希表不支持范围查询
二叉树
二叉搜索树
每次查询的时候,如果查询的值小于当前结点那么向左遍历,如果查询的值大于当前结点那么向右遍历
二叉搜索树在保持平衡的情况下查询速度也是可以达到 O(logn) 级别的;但是二叉搜索树通常是无法保持平衡,所以很有可能退化成链表,最后导致查询的时间复杂度退化到 O(n) 级别,并且二叉搜索树也是不支持范围查询的
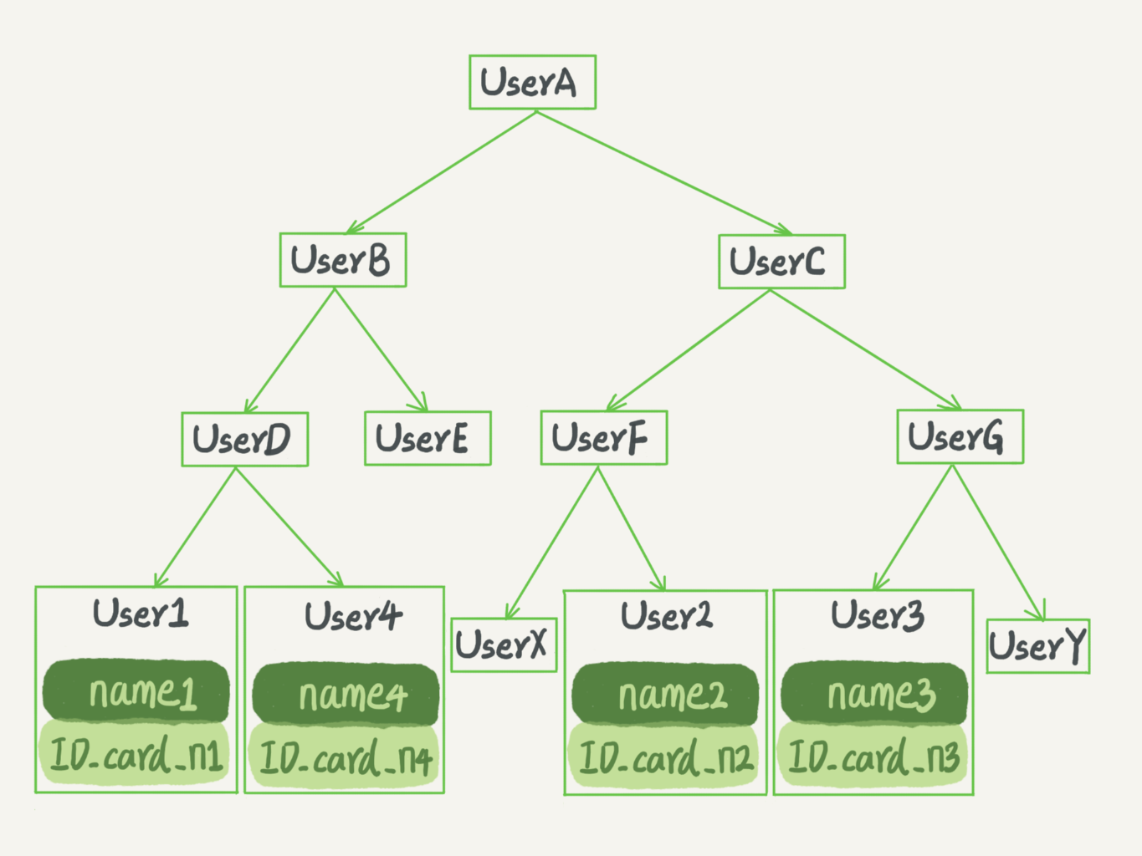
二叉平衡树
注:二叉平衡树的查询原理有兴趣就去看下吧,AVL 树会相对简单,红黑树只能够用抽象两个字来形容
既然二叉搜索树无法保持平衡,那自然可以想到采用二叉平衡树来保持平衡,确实可以做到查询速度稳定在 O(logn) 级别
但是如果结合数据库的实际情况来看就会发现这种数据结构依然存在很大的问题:
基本所有的二叉平衡树(红黑树、AVL 树)都会存在相应的问题:每次执行插入或删除后都会为了保持自身的平衡从而执行调整的操作;如果数据库插入和删除的操作十分频繁,那么就会导致对内存中的数据频繁的进行调整,这个开销显然是有点大的
二叉平衡树和二叉搜索树还存在共同的问题:
- 每个树的结点都只存储一个值,那么在数据量特别大的情况下就会导致整个树的高度非常大,然后就需要执行非常多次的查询才能够找到符合条件的数据。如果查询的数据已经在内存中,那么查询次数较多倒还可以接受,如果是数据不在内存中,那么磁盘 IO 次数过多显然就是不可以接受的
- 两者都是不支持范围查询的,必须要通过回溯找到所有满足条件的数据
多路查找树
注:B 树相关的原理会比较复杂,这里就不去详细介绍,感兴趣的可以看下我提供的参考文章
B 树
B 树实际上就是多路查找树,基本可以解决之前所有数据结构存在的问题:
- B 树插入和删除结点的时间复杂度显然也是常数级别的,并且 B 树也是平衡树所以也是可以保证查询的时间复杂度在 O(logn) 级别;不过,B 树并不会在每次插入和删除之后都进行平衡的操作,只会在特定的条件下执行结点的分裂和合并从而保持平衡,所以保持平衡的代价并不高
- B 树每个结点都可以存储多个值并且每个结点可以拥有多个子结点;所以即使在数据量特别大的情况下,也不会导致整个树的高度特别大,那么最终就可以达到减少查询次数的目的,从而减少磁盘 IO 带来的开销
注:100 万行数据,对于二叉树来说树高就为 20,但是对于 B 树来说可能就很小,如果 B 树是四叉树的话,在每个结点仅存储一个值时高度才就只有 10,那么对于真正的四叉树每个结点是可以存储三个值的,那么高度就会更小
B+ 树
B+ 树具有 B 树所有的优点,并且性能会更加优秀:
- B+ 树每个非叶子结点仅存储索引数据而不存储真实的数据,这样每个结点中就可以多存储一个值,每个结点存储的值多了,那么树的高度就会进一步减小,从而再次减少磁盘 IO 的次数,提升查询的效率
- B+ 树无论查询的数据状况如何,都是需要从根结点查询到叶子结点的,查询效率更加稳定;B 树很有可能查询到非叶子结点就找到目标值就直接返回,查询的效率就没有那么稳定
- B+ 树将所有叶子结点都采用双向链表串联起来,从而让范围查询的效率更高;B 树只能够通过回溯的方式查询所有满足条件的数据;并且全表扫描的速度也会更快,只需要找到叶子结点之后顺着链表遍历就行,不需要采用树的遍历方式
B+ 树也不是完全没有缺点的,在结点中值的数量过少的时候会和其他结点进行合并从而确保结点中值的数量是符合 B+ 树要求的,而在结点中值的数量过多的时候就会自动分裂成两个结点,每个结点存储部分值,这两个操作对应到数据库中就是页分裂和页合并,这个不仅是非常消耗性能的而且会导致数据页的利用率降低(B 树自然也有这些问题)
索引类型
注:要注意每个存储引擎支持的索引都不同,不要认为只有 InnoDB 才支持索引,也不要认为只支持 B+ 树作为索引
InnoDB:
- 支持 B+ 树索引,哈希索引,倒排索引这三种数据结构去实现索引
- 常见的聚簇索引,非聚簇索引,前缀索引,覆盖索引,联合索引都是采用 B+ 树实现的索引
- 哈希索引是采用自适应的方式实现的,也就是会在 B+ 树实现的索引基础之上自动再建立一个哈希索引,我们是无法直接给表中的字段创建哈希索引的,全部取决于存储引擎自身
- 不是非常常用的全文索引就是采用倒排索引实现的,倒排索引在搜索引擎中会使用得更多
注:Memory 存储引擎是可以直接给字段创建哈希索引的,MYISAM 存储引擎则是天生支持全文索引
